

In 1973-1974 the late Dr. Kenneth D. Keele, M.D., F.R.C.P. and the author reconstructed some of Leonardo's descriptions of perspective in order to determine whether these had an experimental basis. It was found that they did. The possibility that they had simply been thought experiments was excluded because some of his claims were so unlikely that they had to be tested in order to make sense. The experiments led to a long term cooperation: first two years together as Senior Research Fellows at the Wellcome Institute for the History of Medicine (London); then with intermittent visits during the seven years while the author was at the Herzog August Bibliothek (Wolfenbüttel). As work progressed Leonardo's method became increasingly evident. The challenge of communicating this method inspired Dr. Keele to write Leonardo da Vinci's Elements of a Science of Man and led the author to write his Leonardo Studies I-II.
There have also been several attempts to make the results of these studies more accessible. In 1981 there was a published lecture on Visualisation and Perspective at the world conference on Leonardo e l'età della ragione (Milan). Here there was great enthusiasm for the sequences of diagrams, which showed a methodical approach, but the criticism was made that the order had been imposed after the fact. Rearranging Leonardo's notes did not prove that he was not chaotic: it heightened the suspicion that he was. Further study led to new evidence that this method was not merely wishful thinking, but very much a part of Leonardo's approach. This led, in February, 1984, to three lectures on Leonardo's method at Brigham Young University, organized by the kind efforts of Professor Dan Blickman. The next impulse came unexpectedly in December 1989 through an invitation to organize, with Dr. Michael Sukale, a section at the European Forum (Alpbach) on Leonardo's Laws of Vision and of Nature. By way of preparation the notebooks were reread and this brought to light Leonardo's lists with their systematic play of variables. An essay was written in haste, which was not suited to the format of the proceedings in Alpbach. So it was distributed to a few friends for criticism and allowed to mature. What follows is the result.
Originally a lecture at the Ateneo di Brescia, "Struttura e metodo nei manoscritti di Leonardo" sponsored by the Centro di studi Leonardiani, Brescia, April, 1991. Published as a book: Brescia: Centro Ricerche Leonardiane, 1993. Revised March/April 2004. Redesigned and made available online in 2021.
The final version of this essay was written in ten days, but the work on which it is based covers nearly 20 years. This would not have been possible without an extra ordinary amount of support. At the outset a doctoral fellowship from the Canada Council permitted me to work in London (1971-1975). This was followed by a senior Research Fellowship from the Wellcome Trust (1975-1977). The seven years of research at the Herzog August Bibliothek in Wolfenbüttel (1977-1984) saw a series of fellowships from the Volkswagen, A. Von Humboldt, Thyssen and Gerda Henkel Foundations. Next came a year at the Getty Centre for Art History and the Humanities (1986-1987), since which time there has again been support from the home base through a Canada Research Fellowship from the Social Sciences and Humanities Research Council of Canada (1987-1992). I am very grateful to these bodies both for their individual support and for the cumulative effects which their help has brought. I am grateful also to the Institute for the History and Philosophy of Science and Technology in Victoria College at the University of Toronto, which has been my base for the past seven years.
Those who are not inclined to write by nature need encouragement and sometimes persuasion to arrange their material for a public audience. Hence I am thankful to the organizers of the 1981 conference in Milan, to Professor Dan Blickman who organized the three lectures at Brigham Young; Dr. Michael Sukale who was so kind in making arrangements for the six lectures at Alpbach and to Ing. De Toni for making possible this publication. I am deeply indebted to my friend Dr R. N. D. Martin who painstakingly read through the draft and helped transform a series of lectures into a statement.
Leonardo da Vinci (1452-1519) has evoked two fundamentally different responses: one sees him as central to early modern science, another dismisses him as an eccentric with no influence. Both views were found while he was still alive. For instance, Pacioli (1509) praised him as being among the most perspicacious of architects and engineers, an assiduous inventor of new things, famous for sculpture and painting, for his construction of the horse, the Last Supper and for his writings: that he was working on "an inestimable work on local motion, percussion, weights and all the forces, that is, accidental weights, having already with great diligence finished a worthy book on painting and human movements."[1] Aspects of this view were kept alive by Venturi (1797)[2], Solmi (1905)[3], Uccelli (1940)[4], Reti (1974)[5] and Keele.[6] On the other hand, Castiglione (1528)[7] criticized him indirectly for frittering away his time on useless mathematical speculation. Serlio (1545) made a different claim: that Leonardo was too much of a perfectionist and that this kept him from publishing.[8]
Twentieth century scholars such as Marie Boas Hall argued that because he never published he had no influence[9], while one recent scholar has dismissed him as "an ingenious empiricist working in an intellectual vacuum."[10] Was Leonardo merely a recluse working on his own out of touch with the great traditions; an over ambitious amateur making notes without any underlying method and structure? This paper shows that Leonardo was widely read and in contact with some of the major scholars of his day. A survey is made of his extant treatises to confirm that these are much more structured than is at first apparent. His plans for books are examined to discern how he intended to arrange his material. It is shown that for all his universality Leonardo focussed on a surprisingly small number of basic themes; that although Leonardo's study of the natural world includes physics, biology and botany he treats them all in terms of mechanics. A detailed reading of his notebooks reveals that he was guided (and inevitably sometimes misguided) by a clear method. The notebooks also contain proof that Leonardo did not write them solely for private study; that he specifically intended them for other readers and had plans for publication. Finally, it will require a survey of historiography to understand how all all this could have been forgotten, with the result that scholars have claimed that he was a peripheral figure, when in fact Leonardo's method is of central importance to the western tradition.
The evidence of Leonardo's notes and correspondence is of a man with wide contacts and reading. Sometimes he cites oral reports. In the Madrid Codex he reports that Julius had seen a case of a wheel being worn out while in Germany.[11] He also considers letters. In one of his prophetic statements he mentions "Writing letters from one country to another. Men will speak from very remote countries to one another, and reply."[12] He writes business letters to his employers such as the Duke of Milan and the Pope. Letters are also one of the ways he searches for evidence, as when he reminds himself to write to Bartholemew the Turk on the question of tides and specifically about the Caspian sea.[13]
Leonardo is also a reader of books and often he cites the evidence that he finds in these. Sometimes he refers generally to Aristotle's De caelo [14] or Euclid's Elements.[15] Sometimes he refers to a specific book and chapter of Aristotle's Physics [16] or to given propositions in Euclid. At least twenty propositions ranging from books 1 to 5 of the Elements are cited explicitly[17]. In his study of ancient weapons in the Manuscript B he cites a wide range of ancient authors: Pliny[18], Virgil[19], Lucretius[20], Aulus Gellius[21], Livy, Plautus, Flavius[22], Lucan, Caesar[23], Quintilian, Varro[24], Plutarch[25], Hermes Trismegistus, Pompeius Festus[26], and Ammianus Marcellinusi[27]. Elsewhere he cites Plato[28] and Vitruvius[29]. Mediaeval sources include Swineshead[30], Thabit ibn Qurra[31], Peckham[32], a Treatise on the abacus [33], as well as Biagio Pelacani da Parma.[34] Contemporary sources include Leon Battista Alberti.[35] We know that he had a personal collection of 119 books.[36] We know also that he did not limit himself to the books he owned himself. There are numerous references to books in other collections. For instance he takes note of a copy of Witelo which is said to be in the library at Pavia[37] and a copy of Archimedes in from the Bishop of Padua[38]. This is not exactly an intellectual vacuum, especially in 1494, four decades after the advent of printing.
In addition to books and correspondence there were his direct contacts with contemporaries. He studied and wrote in the margin on seven pages in one of Francesco di Giorgio Martini's manuscripts (Florence, Cod. Ashburnham 361). In 1490, he travelled with this engineer to Pavia to visit Fazio Cardan, the learned editor of Peckham's Optics and father of Jerome Cardan. In 1494 he bought a copy of Luca Pacioli's Summa and subsequently worked together with this mathematician for three years at the court of Milan (1496-1499). At the same court, Leonardo was "as a brother"[39] with Jacopo Andrea da Ferrara, a leading architect and Vitruvian commentator of the time. As an employee of Cesare Borgia he was a colleague of Machiavelli. In the period 1508-1510 he appears to have worked with Marc Antonio della Torre a professor of anatomy at Milan. In Rome (1513-1515) he worked for the Pope on a sixteenth century version of the star wars project, using burning mirrors as described by Archimedes as a means of defence. The fame of his activities caught the attention of the King of France who persuaded Leonardo to move to France for an early "retirement". The curriculum vitae of a recluse would look somewhat different.
Both the size and contents of the notebooks vary considerably. There are tiny pocket-size booklets such as Forster III (9 x 6.7 cm) or Manuscript H (10.3 x 7.2 cm)[40] and large folio sheets such as the Codex Atlanticus and Windsor. In terms of contents the notebooks fall into three different kinds: travel notes, study notes and draft treatises.
When he travels Leonardo likes to make notes and he recommends this practice to his students[41]. Manuscript L is a good example. Here Leonardo does some surveying, sketches the lay of the town at Cesenatico, notes architectural features at Urbino etc.[42] A second category of study notes is based on both experiments and books, and involves gathering material for his basic themes. Some of this material was unbound. It is likely that Leonardo kept two large piles of unbound notes in his study: one devoted primarily to the man made world (machines, inventions and architecture), now the Codex Atlanticus; the other dealing mainly with nature (anatomy, botany and geology) now in Windsor. This division was not strict. After Leonardo's death, Pompeo Leoni attempted to sharpen the distinction between these two piles by cutting out various portraits and caricatures from the Codex Atlanticus and adding these fragments to the Windsor collection, as Carlo Pedretti has so elegantly shown.[43] There is evidence that Leonardo planned to have what is now the Windsor Corpus [44] bound, but this did not happen during his lifetime. Around 1508 the materials for what is now the Codex Arundel were also in an unbound state, although a note on Arundel 190v [45] mentions that he plans to have this bound also.
The number of topics dealt with on these loose sheets varies. A few contain many themes. A number of sheets contain two or three topics. The majority of sheets are dominated by or deal exclusively with one topic. There is, however, a spectrum of ways in which a theme is treated. In early stages of formulation, diagrams and texts are scattered indiscriminately (e.g.pl.1ab). In a further stage, there is some order. Then there are sheets with some evidence of numbering. Next a pattern of texts with illustrations or vice-versa emerges. Finally we find sheets showing a single example sometimes with an accompanying text. Some of these are presentation drawings intended to be shown separately (cf. pl. 2ab), while others become parts of treatises. In the notebooks which are bound, most folios deal with a single theme and this usually continues over a number of pages. Indeed the majority of the manuscripts are dominated by only a few themes. As Leonardo's ideas evolve he copies them or has them copied into another manuscript, crossing out the original passage involved (pl. 3-4). A note at the beginning of the Codex Arundel suggests that it was drawn up in this way. In the case of the Treatise of Painting, Melzi added a sign alongside passages that he copied from manuscripts such as BN 2038, A, E and G.
Leonardo's earliest bound notebooks, the Codex Trivulzianus (1487-1490, 21 x 14 cm), Manuscript B (c. 1488-1490, 31 x 22 cm) and Manuscript A (c. 1492, 21 x 14 cm) are large in size,and generous in their use of paper. But paper must have become increasingly scarce. On rare occasions, such as CA206ra (549r, c. 1497), Leonardo proceeds in palimpsest fashion, writing over a passage with a new topic. Elsewhere, especially in the Windsor Corpus and the Codex Atlanticus, we find instances where he seems determined to use every inch of space. This is partly because he keeps returning to a sheet in order to add further notes on a given topic, which explains why the dates of these two manuscripts range from the beginning to the end of his career.
Some of the bound manuscripts can be described as study notes insomuch that the order of the folios remains implicit. Manuscript A, which contains his treatise on perspective is an example. The treatise begins on A36v. There is a number 4 at the bottom of the folio, which is repeated at the top of A37r. Similarly at the bottom of A37r there is a 5 which is repeated at the top of A37r. These are the only formal clues of sequence. But as I have shown elsewhere[46] the argument proceeds methodically from 36v through to 42v, thus comprising a short, thirteen-page treatise. A second such treatise is found in Forster II. It goes backwards beginning at 158v and ending at 65v. There is an independent numbering to help us. Hence, folio 158v is 1, 157v is 2...68v is 91, 67v is 92, 66v is 93 and 65v is 94. This accounts for the cryptic note in Latin: "Most powerful mechanics, beginning at the end."[47] Another instance is found in Manuscript M, where a discussion on motion and percussion continues in sequence from 94r to 93v and so on to 90r, thus making a brief treatise of nine pages.
There are also notebooks in which order remains mainly implicit except for isolated passages which give hints of a larger plan. An example is Manuscript F which contains a draft of a chapter for his treatise on cosmology. A note on F94v outlines the overall purpose of the book:
My book sets out to show how the ocean along with the other seas, with the help of the sun, makes our planet reflect light the way the moon does and from a greater distance appears like a star, and this I prove.[48]
By way of introduction Leonardo feels he must establish that the eye is not being deluded when it looks at the sky. So he writes a chapter on optics. This begins on F95v. At the bottom of the paragraph he writes: "It is not possible to define this here for lack of paper, but go to the beginning of the book [i.e., chapter] at folio 40 where this is defined."[49] At folio 40 the treatise continues and proceeds backwards to 39v,39r and so on through to 28r. I have made a complete analysis of this treatise elsewhere.[50] It is important for our purposes here to note that Leonardo also uses this method with respect to other themes discussed in the same manuscript. On F13v, for instance, he writes "Turn the page."[51] On F26v he writes "Here follows the proof of that which is said on the page opposite."[52] On F52r he notes "Go to page 59."[53] All this is not simply because he is being obtuse. These were times of war. Paper was in great shortage. There were many interruptions. These were his working notes. But even so, he too wanted order.
Similar notes are found in two other manuscripts. In the case of Manuscript E, the page sequence again is frequently the opposite of his argument, i.e. he starts at the back and works forward. Hence, when on E75r he writes "Here is finished what is lacking three pages before this,"[54] We need to go to 77r to find the relevant passage. Manuscript G contains at least seven notes of this kind. On G44v Leonardo writes "And this is drawn in the margin at the bottom four folios following[55]," i.e. G48r. On G46r he writes: "Here follows what is lacking on the page opposite"[56], i.e. 45v. On G46v he notes: "Read page 45[r]."[57] On G51v he writes "go to page 44."[58] On G67r he explains that the text continues on the page opposite at the bottom[59], i.e. 66v. On G75r he adds two notes: "Here follows what is on the opposite page[60]," i.e., 74v at the top, and also "the round beam is drawn on the page opposite."[61] Finally on G80r there is a similar note.[62] The sequence of his argument is much more erratic in G than elsewhere. He is working in Rome at the time (1513-1515), and developing his pyramidal law with respect to mirrors[63], precisely the kind of information that the German industrial spy, Johannes, the mirror maker, was trying to steal. I suspect that Leonardo was in this case consciously giving a superficial impression of chaos.
In a third kind of manuscript Leonardo uses part or even a whole manuscript to gather material related to a specific topic. This kind of treatise confirms that Leonardo is capable of more coherent and systematic presentation. An early example is Manuscript C (c.1490-1491), which deals with light and shade. The most interesting example is Forster I (c. 1505). A note in mirror script on Forster I 3r informs us that this is a "book entitled on transformation of one body into another without diminution or augmentation in material."[64] This note has been rewritten in ordinary script by a later reader. A note on 3v, which has again been rewritten in ordinary script informs us that this manuscript was "begun by me, Leonardo da Vinci on the 12th of July 1505."[65] The actual treatise begins on 39v with a proposition numbered "1st." On 39r a 2nd and 3rd proposition follow. These continue in order until proposition II on 35r. From 34v through 28v (pl. 7-8) there is a second series of 13 numbered propositions. From 28r through 20r there is a third series of 20 numbered propositions. His numbered list of 28 geometrical transformations cited earlier gives us another glimpse of the order he had in mind. The latter part of Forster I, namely folios 40v through 55r, deals with a distinctly different topic, hydraulic machines. Here the diagrams are much rougher and the general impression is more chaotic. If we look closely, however, we find that beginning on folio 45r the diagrams are numbered 1, 2 and respectively. On 45v we find the numbers 4, 5 and 6. This continues in orderly fashion until numbers 41 and 42 on 53r.
This principle of numbering the illustrations by way of establishing the sequence of his ideas recurs in Madrid Codex I, this time in the context of weights and balances (pl. 5-6). On Mad I 190r Leonardo adds to his illustrations the numbers 3, 4, 5 and 6. This sequence of numbers continues in the opposite direction of pages such that we find illustration 100 on folio 172r. This sequence then begins a fresh on this same folio 172r with figures 1 and 2 and continues until figure 90 on folio 158r. In Manuscript K, beginning on 79r, this time in the context of geometrical diagrams we find two numbered propositions which continue in sequence until 14 on folio 73r. A late example of this approach is Manuscript D (c.1508), on problems of vision.
As will become evident, by 1492 Leonardo had developed an explicit method for presenting his ideas that was reminiscent of the form Euclid established for classical geometry: a proposition (i.e. a claim), followed by demonstrations (i.e. examples based on experiment or at least experience), frequently accompanied by illustrations to show different possibilities. In the notebooks, the propositions increasingly serve as headings for demonstrations in paragraph form accompanied by diagrams, often in the margin. This procedure is seen clearly in Codex Leicester (now Hammer) and Manuscripts E, F and G. Sometimes the margins give summary versions of the proposition, as in Manuscript D. Hence, in addition to his travel and study which are frequently without a planned order, Leonardo has a clear method of presentation when he begins to organize these with a view to creating formal treatises[66].
Besides this physical evidence there are clear references in Leonardo's notebooks to specific books and propositions. Some of these are in the Codex Atlanticus. On CA384ra (1493-1495), for instance, Leonardo mentions: "I stated in the 7th conclusion how percussion...."[67] On CA155vb (1495-1497) he asks us to "look at the 7th [proposition] of the fifth [book] of the axle and the wheel."[68] On CA2ra (1515) we find a precise reference to his book on machines discussed earlier:
Since without experience one cannot give true science of the power by means of which the drawn wire resists that which draws it, I have drawn here, on the side, these four motor wheels of the perpetual screws, marking the degrees of power alongside each one. These powers are true as is proved in the 13th [proposition] of the 22nd [chapter] of the elements of machines written by me.[69]
Another late note on CA287re (c. 1514-1515) informs us that "Mr. Battista dall'Aquila, private secretary to the pope, has my book in his hands."[70] In the Codex Arundel, on folio 12r, Leonardo refers us to "the 5th of the 7th"[71] in connection with weights. On Arundel 25r, he mentions "as proved in the 4th of my [book on] perspective."[72] On Arundel 25v he refers to "book 9 of water".[73] Sometimes the references are laconic as on K30r to a "sixth book"[74] or in Manuscript F where there are at least four references to "book 9 on water" on folios 5r, 24v, 72v and 88r respectively, two references to a "book 10 on water" on folios 4v and 24v, plus headings on 35r for "Book 42. On rain"[75] and on 37r for "Book 43. On the motion of air included below water"[76], as well as a simple note on 66v: "Beginning of book [of water]."[77] On Manuscript I 72v there is also a: "Beginning of book on water."[78] On E59v (1513-1514) there is a: "Beginning of this book on weights"[79] and on E27v there is a note: "proved by the ninth of percussion."[80] On W19061r (K/P 157r) we read: "proved by the 5th on force."[81] Leonardo also refers on W19061r (K/P 154r) to the "order of the book [of anatomy]....Hence with these 15 entire figures the cosmography of the microcosm will be shown to you with the same order as Ptolemy used before me in his Cosmography".[82] Thus Ptolemy's method of arranging the macrocosm serves as a direct model for how Leonardo arranges the microcosm. On W19009r (K/P 143r) Leonardo refers once more to his book on machines:
Make sure that the book on the Elements of Machines with its practice comes before the demonstration of motion and force of man and other animals, and by means of these you can prove all your propositions.[83]
In addition to the above evidence of books actually written or at least in progress, there is considerable evidence of plans for books. On rare occasions such as Mad I 173v (c. 1499), we find him making a note on method: "You will put the whole text together and then you will divide it and add the commentary."[84] Then there were plans for specific subjects: painting, perspective, cosmology, transformational geometry and machines. The book on machines included his work on the four powers of nature (force, motion, percussion and weight). From a note on CA117re (1490) we know that he had begun planning this work at an early stage in his career: "First you will deal with weight, then with motion which gives birth to force, then you will deal with force and finally with percussion."[85] A few years later on CA149rb (1493-1495) he elaborates on his plan:
Beginning of the nature of weights.
The plan of your book will proceed in this form: first the simple beam, then supported from below, then partly suspended, then entirely, then these beams will support other weights.[86]
In the decades that follow this evolves into a major treatise which deals with the theory and practice of machines (cf. pl. 25-26) and their relation to the four powers of nature, all of which serves to introduce his treatise on human and animal movement. A separate book was planned for the flight of birds. The Codex on the flight of birds now in Turin is but a fragment of the projected work as we learn from a passage on K3r (after 1504):
Divide the treatise on birds into 4 books. The first will be on flying by flapping their wings. The second will be on flight without flapping thanks to favourable winds. The third will consider principles of flight common to birds, bats, fish, animals and insects. The final book will deal with instrumental flight.[87]
Image 64a
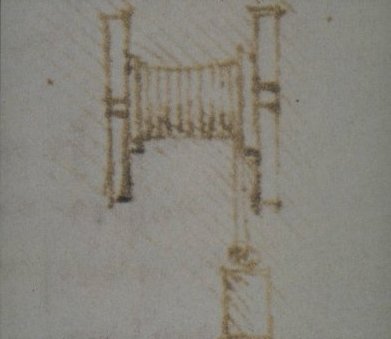
image 64b
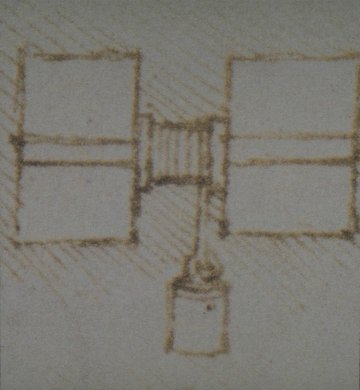
Image 69a
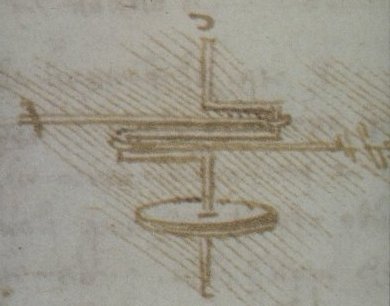
image 69b
Instructive in this context is Madrid Codex I where we find a number of references to specific books and propositions. On Mad. I 105v-106r, for instance we find a series of (almost) consecutive propositions. Sometimes he provides the name of the book in addition to book and proposition number as when he refers to "Bk.5.3 of motion and percussion" (moto e colpo) on Mad. I 69v; "Bk.7.5 of motion and force" (moto e forza) on 94r; "Bk.7.5 and 9.7 of his theory" (teorica) on Mad. I 140v. Sometimes he simply refers to a proposition number without reference to book number as in "5th of theory" on Mad. I 147v, "5th" on Mad. I 71v, "6th" on Mad. I 87r and "7th" on Mad. I 140v. In 33 cases he gives book and proposition number[88]. If Leonardo were truly as chaotic as he is generally assumed to be there would be little incentive to refer so often to specific books and propositions. On F41v (c. 1508) Leonardo outlines a slightly different plan:
To speak of such material you need in the first book to define the nature of resistance of air. In the second the anatomy of the bird and its feather. In the third the operation of such feathers through different motions of their own. In the fourth the value of wings and tail without flapping the wings with the aid of different headwinds in steering with different movements.[89]
Water was another theme about which Leonardo planned to write a major work. On F90v [90], F45v [91] (c. 1508) and E12r [92] (1513-1514) he makes notes concerning the order of topics in this work. On F87v he describes his general plan:
First write everything about water in each of its motions and then describe all the surfaces over which it flows and their materials always adding the propositions of the aforesaid waters and let it be in good order otherwise the work will be confused.[93]
Much more elaborate plans are found in the Codex Atlanticus. These are striking because they again reveal the sytematic play of variables that we have identified as an essential element of his method. On CA79ra (c. 1505-1506), for instance, Leonardo makes a list headed:
Book on the percussion of water with various objects
Encounters of water with permanent objects of different shapes that overcome the water
Encounters of water with immobile objects covered by water
Encounters of water with mobile objects covered by water
Encounters of water with permanent objects that overcome the water
Encounters of water with pliable objects that are overcome by water
Encounters of water with objects which fall with a circular motion such as wheels of aquatic instruments.[94]
On CA74v (1505-1506) Leonardo makes further lists, among them one on different kinds of eddies:
Eddies which are superficial
Eddies which rise from the bottom to the surface
Eddies which go from the surface to the bottom
Eddies which move with the course of the stream
Eddies which change direction, as those in ebbs and tides of rivers
Eddies which are lateral and continuous
Eddies which are lateral and discontinuous
Eddies which are wide above and narrow below
Eddies which are narrow above and wide below
Eddies which are straight from bottom to top
Eddies which are oblique from bottom to top
Eddies which are very large
Eddies which are small
Eddies which have gurgles
Eddies which are pipe-like
Eddies which are screw-like
Eddies which are hollow and filled with air
Eddies which are not hollow[95]
Leonardo made further such lists both in the Codex Atlanticus [96], Codex Arundel [97] and the Codex Leicester (now Hammer).[98] Indeed, as Carlo Pedretti has claimed Leonardo made a series of references to a now lost treatise, Codex M [99], which dealt with problems of water. What emerges, therefore, is a much more coherent picture than is usually ascribed to Leonardo. We shall see that this applies equally to the basic themes on which he focusses his attention, and the method which he uses in dealing with these themes.
Far from being just a wild enthusiast making notes about everything possible, Leonardo is surprisingly specialized in his studies. Moreover, the basic themes which he chooses are guided by systematic principles. It is striking that only about 10% of Leonardo's extant notes are about the natural world. Nearly 90% of his notes are concerned with man-made worlds which can be divided into mental, represented and constructed worlds. Of these the mental world receives about 15% of his attention, the represented world approximately 20%, while the constructed world receives approximately 65% of his attention, if we judge on the basis of extant notes.
Leonardo's study of nature focusses on three aspects: physical, biological and botanical. With respect to the physical world, he is guided by two interests: cosmology and physics. He wishes to write a major treatise on the nature of the universe[100]: to show that the moon reflects the sun as does the earth; that the moon has oceans like the earth (pl. 32) and that from a greater distance both the earth and moon look like stars. This is why he spends at least 20 pages on the problem of the sun's image in water. Leonardo insists, moreover, that the earth is in the centre of its elements rather than in the centre of the universe. Thus he can argue that the moon is in the centre of its elements and that the same applies to the other planets. In so doing he challenges objections that water and other elements on the moon should fall back to earth. This rejection of the geocentric model of the universe before Copernicus is of interest in its own right, but for the moment we must limit ourselves to the structure of his thought. In order to be certain about the nature of the earth requires some attention to geography, geology, the nature of tides and meteorology. To be certain of the nature of the heavens requires some attention to astronomy. Here Leonardo focusses interest on the moon: its appearance, substance, its phases. To certify that he is not being deluded in what he sees, requires study of optical principles. His studies of the eye in Manuscripts D and F were intended as chapters in the treatise on cosmology. His studies of optical instruments, notably mirrors, eyeglasses and a prototype of the telescope, were also part of this enterprise.[101]
Leonardo's second motive for studying the physical world lies in his physics. Here he is guided by his concept of four powers of nature (force, weight, motion and percussion), which he treats mechanically and by means of which he intends to gain a new understanding of the four elements: earth, water, air and fire. With respect to the natural world he focusses on two powers, motion and percussion, in conjunction with one element, water. This is no coincidence. Given his principle of limiting himself to study of visible phenomena, water provides him with the best medium for studying both motion and percussion. Water is of practical interest with respect to canals, irrigation, etc. It is also of theoretical interest. Leonardo sees water as a slow motion version of air. As early as 1490 he claims of CA361va: "Wind has similarity with the movement of water."[102] This has consequences for his study of both the natural and the man made world. On M83r (before 1500) he notes "swimming shows the way of flying"[103] a thought he restates in CA66rb (c. 1505). "Swimming in water teaches men how birds do it in air."[104] "He elaborates on this line of reasoning on E54r (1513-1514):
In order to give a true science of the motion of birds in the air it is necessary first to give the science of winds which you prove through the motions in water and this science of a sensible nature will serve as a ladder in gaining cognition of birds in air and wind.[105]
These same assumptions have important consequences for his biological studies, where he studies man, horses, some other animals (e.g. dog, donkey, bear), birds, insects and fish, but largely from a viewpoint of their underlying mechanical principles of motion. Instead of making catalogues of birds, he studies how they fly. Instead of making catalogues of fishes, he examines how they swim. So too with horses: he focusses attention on how they run. Moreover, all these studies have an ulterior motive, aside from providing him with subjects for painting: to improve man's ability to move through the elements with mechanical equivalents of running, swimming and flying (see fig. 2).
| Earth | Water | Air | |
|---|---|---|---|
| Earth | Water | Air | |
| Man | * | * | * |
| Horse | * | ||
| Fish | * | ||
| Bird | * | ||
| Motion | Running | Swimming | Flying |
| Mechanical Equivalent | Cart | Boat | Mechanical Bird |
Once these connections are recognized, Leonardo's emphasis on human motion in his anatomical studies takes on new meaning. So too does his decision to preface these studies with his work on machines and the four powers, as does his concern with particular machines such as carts, boats and mechanical birds. Leonardo is neo-Platonist insomuch that he is fascinated by the traditional microcosm-macrocosm analogy. At the same time he is guided by what might paradoxically be termed a mechanical anthropomorphism which helps us to understand other features of his work. On A55v (1492) he compares the body of a man with the body of the earth.[106] On A56r (1492) he compares the veins of man with the underground rivers of the earth.[107] Even much later, on CA5260ra (c. 1508-1510), he compares the lungs of man with those of the earth.[108] Cited out of context, as they often are, such passages make Leonardo look thoroughly committed to outdated classical and mediaeval organic cosmological metaphors. But this ignores the mechanical context, which he assumes for both man (microcosm) and world (macrocosm).
In the Windsor Corpus he refers repeatedly to the human body as an instrument as on W19029r (K/P 71r) where he mentions the "wondrous instrument invented by the consummate master"[109], or W19037r (K/P 81v), where he announces that he will "demonstrate this instrumental figure of a man in 24 figures."[110] Leonardo's view of birds is analogous, as is clear from a passage on CA161ra (c. 1505): "The bird is an instrument operating by mathematical laws, which instrument it is within the power of man to make with all its motions but not with as much power."[111] Similarly, Leonardo looks upon the earth as a machine. On W19147-8r (K/P 22r) he mentions it as a "terrestial machine."[112] On CA269ra (1490) he states that as a result of "various opinions concerning the size of the spherical terrestial machine, I have become concerned to create or rather to construct an instrument which will adopt this form."[113] Here he is speaking of a surveying instrument. On CA252rb (1490-1492) he refers to this "terrestial and worldly machine[114]," and on A59v (1492) to "the universal machine of the earth."[115] In short, while maintaining some traditional organic metaphors concerning the microcosm-macrocosm analogy, Leonardo treats them mechanically rather than organically.
In addition to anatomy and principles of motion, two other aspects of man are of concern to Leonardo: the senses and reproduction. With respect to the senses he makes some mention of all five. But by far the greatest attention is on sight and this for two reasons. First, sight is the sense that gives access to visible things and the visible is his standard for truth. The study of optics is thus crucial to ensure against illusion and to certify that his experimental observations are as objective as possible.[116] Secondly sight is directly connected with perspective, which serves to demonstrate measurable relationships between what is seen, what is represented and the natural world. Perspective also serves as a bridge between abstract mathematics and the concrete world. In addition it plays a significant role in his painting.[117] Hence optics and perspective remain leitmotifs throughout Leonardo's writings.
Leonardo also has some interest in the problem of sexual reproduction and devotes a few pages to the relevant male and female organs, and to the problem of a foetus in the womb. This constitutes such a small fraction of his work that it would not deserve mention here were it not for a curious analogy which Leonardo sees between the umbilical cord of a newborn child and the flowers and blossoms of certain plants. Indeed his attention to the botanical world, which includes trees, plants and flowers[118], focusses in very large part on the question of plant reproduction: blossoms, flowers, fruits, seeds. As in the biological world instead of making catalogues of genera and species, Leonardo's attention is focussed on a specific problem. And once again it is guided by his study of man and woman.
Hence, although Leonardo's study of the natural world includes physics, biology and botany, he treats them all in terms of mechanics. Indeed, he focusses on man and the universe to create a mechanical version of the microcosm-macrocosm analogy. This is one of his central concerns even if it involves only a small fraction of the notebooks.
Leonardo's interest in the mental world is primarily in terms of principles of communication which he would see as threefold: numbers (arithmetic), words (language) and diagrams (geometry). His work in arithmetic amounts to about 1% of his notes[119] and is limited almost entirely to arithmetical proportion, practical problems deriving from the abaco school[120] and some computations. Words in terms of language[121] and literature[122] (cf. figure 2) interest him more and constitute roughly 4% of his notes.
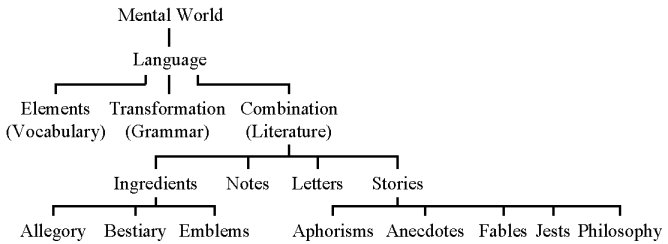
Much more important are his studies of geometry. When Leonardo praises mathematics he usually means geometry[123] and sometimes geometry in combination with mechanics. Through his study of perspective (c. 1488-1492) Leonardo becomes interested in both geometry and geometrical proportion. When Pacioli's compendium on the subject is published in 1494 Leonardo buys his own copy. From 1496 through 1499, Leonardo draws illustrations for Pacioli's Divine proportion later published in Venice (1509). Like Pacioli, he sees proportion as a key to nature. But Leonardo is more concerned with earthly proportion. As he states on K49r (after 1504): "Proportion is found not only in numbers and measures, but equally in sounds, weights, times and sites and every power that exists."[124] Even so, proportion is but one of the branches of geometry that interests him (cf. fig. 3). Pacioli leads him to study Euclid[125], whose Elements deal mainly with geometry in two dimensions.
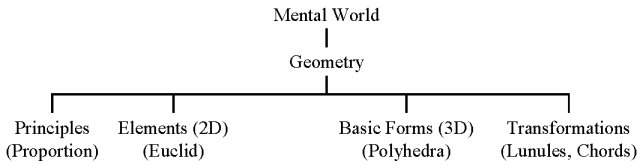
Leonardo's study of perspective prompts him to explore three-dimensional treatment of geometrical forms. In his treatise on the geometrical game[126] he limits himself mainly to the five Platonic solids. Elsewhere he explores most of the 13 Archimedeian solids. For Leonardo transformational geometry involves an infinite variety of shapes and he sees them almost literally as building blocks of reality. Moreover, because these changes are reversible and repeatable they serve to demonstrate his concept of science.[127]
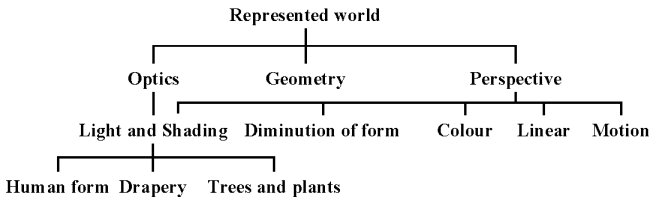
One of the reasons why Leonardo's work is not in a vacuum is because it is related to his professional concerns as a painter. Hence, in addition to the mental world with its branches of arithmetic, language and geometry there is the represented world to which he devotes his Treatise of painting. Leonardo sees painting and science as intimately connected because painting creates bridges between geometry and nature and helps to record visible evidence, which is his key to truth. Perspective plays a central role in this process, while optics and geometry are also significant. Optics provides him with the laws of light and shade[128] by means of which he can deal with human forms[129], drapery[130], trees and plants[131], and geometry provides him with the principles of transforming their shapes (fig. 4).
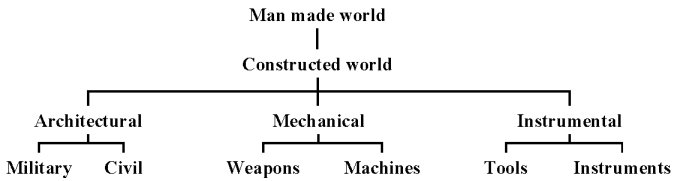
Yet the focus of Leonardo's attention is in the constructed world which includes architecture[132], mechanics and instruments (fig. 5). In his architectural studies we find him playing systematically with basic geometrical forms in the ground plans of his designs for churches (pl. 21-22) in Manuscript B as early as 1490 before he develops the idea of applying a play of variables to nature's powers. Military concerns play some role in his exploration of the constructed world but are more peripheral than one might expect. If his military architecture[133] involves some significant innovations, his weapons[134] are surprisingly traditional. As noted in our discussion of sources, Leonoardo makes a detailed study of ancient military authors and studies contemporaries such as Francesco di Giorgio Martini.[135] This results in his weapons being almost entirely dramatic representations of existing warfare rather than radically new devices.
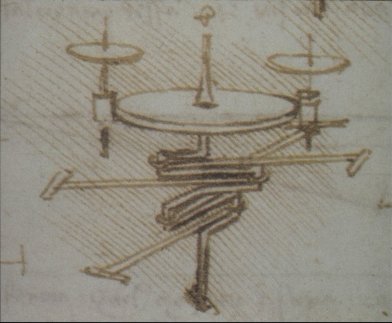
His originality lies in his treatment of machines[136] and instruments. If we leaf through the Codex Atlanticus or the Madrid Codices with no understanding of his method, our first impression is an endless variety of mechanical devices. This is not the case (pl. 25-28). As Reti[137] has shown, Leonardo considers 21 mechanical elements. He is not disordered. Indeed if we examine actual machines we find six basic types that he studies in some detail: pulley, crane (including crane shovel), winch, cart, textile machine and file machine. With respect to water he has three further machines: boat, archimedeian screw and fountain. With respect to air he has his flying machine[138] (see fig. 6).
| Earth | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Hoisting | Dragging | Rolling | Digging | Weaving | Pounding | Weighing | Measuring | Space | Time |
| Crane | Winch | Cart | Shovel | Textile | File | Balance | Compass | Clock |
| Water | |
|---|---|
| Sailing | Boat |
| Raising | Srews of Archimedes |
| Air |
|---|
| Flying |
| Mechanical Bird |
| Fire |
|---|
| Burning |
| Mirror |
Leonardo is trying to catalogue basic mechanical actions with respect to the four elements. Each of these actions involves combinations of the four powers (motion, force, weight and percussion). Hence his study of the constructed world is guided by a simple, underlying purpose: to establish the mechanical principles of the four powers with respect to the four elements of nature. He is also concerned with the principles governing: a) the four powers (pyramidal law); b) geometrical forms (transformational geometry); c) interpretation (optics); and, d) representation (perspective. He is inspired by three goals: to understand the natural world created by God; to construct new man made dimensions of the natural world and to represent new man-made worlds.[139]
If machines inspire him to look for universal principles they do not suffice to demonstrate them. For this he needs instruments, and it is surely no coincidence that he has at least three times as many notes on instruments as on machines. Some are surveying instruments, which we find him discussing in the context of settling disputes and certainty as on CA269va (727r, c. 1490):
Having seen various opinions of the size of this orb, the terrestial machine, I judged that since among so many disputants there were as many opinions, certain truth must be quite distant from them since, if the truth had come to their minds, all would be of one opinion. And given this great diversity of opinion, I decided to create or compose an instrument in this form....[140]
But again most of his energies are focussed on four instruments: mirror (concave and convex as well as plane),[141] clock[142], balance[143], and compass.[144] The regularity of these precision instruments permits him to begin testing his intuitions about the universality of nature's mechanisms in a systematic way, because he can now, under controlled repeatable conditions, check the effects of changing one or more variables. Instruments thus become models for testing whether nature's powers are as regular as he thinks they are. Each of the instruments has its own special use in this process. Mirrors serve to explore laws of light and also, in the case of concave mirrors, heat, both of which Leonardo considers as instances of percussion. Clocks (cf. pl. 4, 25) serve to demonstrate percussion, through the striking action of the lock mechanism, as well as weight, motion and force. Balances are particularly suited to studying properties of weights. Pulleys which are a variant form of balance, allow the study of weight, force and motion. Study of these instruments leads him to think in universal terms. On CA321re (882r, 1493-1495), for instance, he explores "how all wheels are of the nature of a balance."[145] On CA396rd (1102r, 1495), he reminds himself to "make mention of the general rule about the contact of axles and all weights."[146] At the same time instruments offer a way of testing his ideas about all four powers. By the mid 1490's he is planning to write on this as he mentions on CA155vb (421v, c.1495-1497):
First speak of motion, then weight, because it is born of motion, then of force which is born of weight and motion, then of percussion which is born of weight, motion and often of force.[147]
A passage on CA267ra (721r, 1495) confirms that he is thinking in terms of a general rule for at least two of the powers of nature and considering Pythogorean music as an integrating principle: "General rule of percussion. General rule of force. In these two rules, that is, of percussion and force, one can adopt the proportion which Pythagoras uses in his music."[148] Another passage on CA20va (66r, 1493-1495) shows that he is seeking: "To make a general rule of the difference that there is between simple weight and weight with percussion caused by different motions and forces."[149] He pursues this approach on CA 120vc (330av, 1497-1498): "Just as you find a rule to diminish weight with respect to a motive force, you will also find a rule to increase time with respect to motion."[150] This leads to the systematic list in the Madrid Codex cited below.[151]
Meanwhile, as of 1492, he has been developing his laws of perspective. They begin as quantitative demonstrations of systematic changes in the visual pyramid when it is intersected at various points by an interposed plane. These principles apply equally to representation and thus become the basis of his new perspectival laws of painting. This gives him a way of testing changes in visible images. The regularity with which the visual pyramid grows and diminishes becomes, for Leonardo, a model of nature's regularity. He develops a pyramidal law. By about 1500, on CA151ra (407r) he is combining this pyramidal law with his concept of the four powers of nature:
All the natural powers have to be or should be said to be pyramidal, that is, that these have degrees of continuous proportion towards their diminution as towards their growth. Look at weight, which in every degree of descent, as long as it is not impeded, acquires degrees in continuous geometrical proportion. And force does the same in levers.[152]
By about 1503, Leonardo is referring, on CA335vd (915br) to "a treatise of mine on local motion, force and weight," in which he emphasizes the use of instruments and speaks of their particular use and value in producing claims which are confirmed by experience.[153] In a paragraph on CA271re (732br, c. 1508) headed, "On local motion" Leonardo supports his claim by reference to "the fifth of the ninth which states...[154]," from which we can infer that his treatise is by now organized into books and propositions. This is almost certainly the treatise to which Pacioli in his publication of 1509 refers as nearing completion.
Leonardo continues working on these problems and makes plans to incorporate them into a treatise which also deals with more complex interplays of the four powers as we learn from CA81vb (220v, 1508-1510) where in a note "On the elements of machines" he outlines his new plan: [To study] "weight proportioned to the power which it moves one has to consider the resistance where such a weight is moved and of this a treatise will be done,"[155] (cf. pl.27-28). Meanwhile he has been collecting material on each of the individual powers. On CA298rb (818r, 1495) he refers to a fifth [proposition] of the seventh [book] with respect to weights.[156] On CA283vab (771v, 1517-1518) he refers to an "eighth book on weight."[157] This applies also to other powers. On CA384ra (1062r, 1493-1495) he refers to a "seventh proposition"[158] concerning percussion. By the time he is established in Rome he has enough material to organize it into book form as we learn from CA241ra (657v, 1513):
Divide percussion into books of which, in the first one there is demonstrated the percussion of two bodies of which one moves, the percussor to an immobile object; [in] the second book percussor and percussed move reciprocally, one against the other. A third is of liquid materials; a fourth of pliable objects; a fifth...[159]
On CA241vb (657v), i.e. elsewhere on the same folio, following a discussion of weight, Leonardo adds an important note: "The book on impetus precedes this and before impetus goes motion."[160] Impetus is another term for force in Leonardo's scheme. Hence we can infer that by 1513 Leonardo's work has resulted in books on each of the four powers which he intends to arrange in the order: motion, impetus [i.e. force], weight and percussion. About this time we also find him on CA374ra (6043v, 1515) planning to write a book on friction[161] in machines which presumably is intended as a further section in his Elements of machines.
Leonardo has in mind an even bigger picture as becomes evident from two lines of text on CA58ra (161r, 1503-1505): "Of two cubes, of which one is double, the other, as is proved in the fourth part of the Elements of machines composed by me."[162] In other words the Elements of machines which deals with principles of the four powers also deals with principles of geometry and geometrical problems.
At this juncture a digression is necessary. By way of context we need to examine developments in optics and perspective. Ever since Antiquity there had been discussions concerning how one could be certain that the eye was not being deceived. Ptolemy (c. 150) had explored criteria for this. These were examined in much greater detail by Alhazen[163] (fl. 1000-1030). In the Latin West, Witelo (fl. 1260-1280) worked in this tradition and considered astrolabes and quadrants as "instruments for the certification of sight[164]," the assumption being that the eye is readilly deceived and instruments are needed to insure against this. This philosophy was consciously in the minds of those responsible for the great proliferation of scientific instruments[165] in the latter fifteenth and throughout the sixteenth centuries. In this context the perspectival window was, in one sense, merely another instrument for the certification of sight. At the same time it introduced a new factor: an ability to record the image involved in a systematic way. To do this, however, required the use of ruler and compass. In short, perspective not only transformed the way pictures looked by giving them coordinated vanishing points: it did something basic to the process of representation by linking it in a fundamental way with instruments.[166] Moreover, instruments such as the compass had traditionally been linked with proportion and problems of geometry. Hence perspective brought into play a nexus of five unlikely elements: certification of sight, representation, instruments, proportion and geometry.
It was not until the period 1490-1510 that this nexus became apparent largely through the efforts of two individuals. Luca Pacioli played an important role in publishing his great Compendium of geometry, proportion, proportionality (1494), as well as emphasizing religious and metaphysical dimensions in his book on Divine proportion (written 1496-1499, published 1509). Meanwhile Leonardo played a more fundamental role. By 1492 he had demonstrated that perspective involved a systematic play of images which[167], he realized, were geometrical. Hence, visual transformations and geometrical transformations represented on the picture plane were recognized as being the same problem with a common solution: using instruments such as the compass.
By 1500, Leonardo is studying Euclid's Elements in some detail.[168] We know from a much later note on CA174v (476v, c. 1517-1518) that he wants to use Euclid to transform geometrical shapes.[169] Yet his goals are quite different from Euclid. On CA183rb (502r, c. 1500) Leonardo states: "I want to make of a circle an infinite variety of curvilinear figures of equal capacity."[170] At the outset he proceeds as if arithmetical and geometrical approaches are interchangeable in pursuing this goal. On CA141ra (386r, c. 1500-1505), for instance, he notes that "In equally diminishing one and the other extreme of each proportion arithmetically, the geometrical proportion will always increase accordingly."[171] Later he is conscious that there are exceptions, as on CA174va (475v, c. 1517-1518), where he observes: "But this calculation wants to be geometrical because, if you wished to do it by means of arithmetic it would be impossible."[172]
The study of square roots makes him more aware of the value of geometrical proportion. He comes to it relatively late. In 1504 we find him writing on CA120rd (331v): "Learn the multiplication of square roots from Master Luca Pacioli."[173] Four years later he is giving instructions on how to reach a solution and arrive at a rule for both square and cube roots on CA159ra (428v, c. 1508): "With the circle br you will make a rule of the square roots up until 20 and then, with another [circle] you will make another rule of cube roots to twenty and you will see the differences that there is from one rule to the other."[174] Later he simply gives the rule on CA102va (281r, 1516-1517): "If you wish the square root of any number, this is the rule..."[175] (There are hints that Leonardo intended to combine these studies of square and cube roots with the operations of his proportional compass, but no concrete evidence of this is found in manuscripts until some forty years after his death. Printed versions appeared in 1584, 1604, 1605,1606 etc. This nexus of mathematics and instruments goes hand in hand with the rise of trigonometry and is reflected in a title of a book by Bramer: Trigonometria planorum mechanica, 1617).
While Leonardo uses instruments such as the compass from the outset it is noteworthy that he only gradually accepts their validity in arriving at rules which he considers true. On CA231ra (629r, C. 1505), for instance, he makes a geometrical construction with a note: "Make a large one and you will see with greater certainty whether this is true."[176] On the same folio he remarks: "The mechanical proof is true even it if is with difficulty that one finds this truth."[177] Here he is dealing with the problems of two mean proportionals and duplication of the cube. His reference to geometry in his book of machines, it will be recalled, involves this same problem. So Leonardo's Elements of machines clearly has two programmes: one to give principles governing instruments and machines in terms of the four powers, a second to provide principles by means of which instruments can be used to represent geometrical truths and transform them systematically. All this is of particular interest to him because it links up with his standard of the visible and because, in being reversible and repeatable, it exemplifies his concept of true science.[178]
And so a nexus evolves which links instruments, geometry, proof and science. Sometimes, as on CA218va (587v, c. 1503-1505) he simply notes: "here the mechanical proof is given"[179], a phrase which reminds us that Leonardo's reference to mechanics being "the paradise of the mathematical sciences"[180] is something much more than an engineer's enthusiasm for machines and gadgets. It reflects a conviction that mechanical instruments provide new keys to mathematical demonstration and proof. By 1508, on CA220vb (593v), Leonardo is referring to a "geometrical rule."[181] Sometimes he carefully records the date of a new insight as on CA239v (627r) when, in connection with falcates (curved sections of circles used in his transformational geometry) he refers to a "first [proposition] which is found in this rule...on the third of March 1517."[182]
The rules to which he keeps referring become increasingly universal in their scope. On CA103va (285r, c. 1515-1516), for instance, he mentions how the rule in question goes on to infinity[183], a phrase which he also uses in connection with the four powers.[184] A year or two later he is confident enough to speak of general rules as on CA107va (297v, c. 1517-1518): "And concerning this diminution or augmentation one will give a general rule which, as we shall see with precision, has a clear note of the truth."[185] Systematic augmentation and diminution are again terms he uses in connection with the four powers. What is most striking about this passage, however, is the way in which the precision of instruments is implicitly associated with his concepts of general rule and visible truth, through constructed geometrical diagrams. It is hardly surprising, therefore, that Leonardo gradually uses geometrical diagrams as synonymous with the term demonstration.[186]
Proportion plays an ever greater role in this nexus of interests. As noted earlier he bought Pacioli's Compendium of geometry, proportion and proportionality when it was first published in 1494, and like Pacioli, he was convinced that proportion extended to all realms of nature.[187] A note on CA177rb (483ar, c. 1508-1510) mentions "and this is proved in the eighth of proportion"[188], which suggests that he is writing a book on this topic also. Later, on CA166vb (454r, c. 1515) he refers to "a rule to know the value and proportion of many curvilinear parts."[189] Indeed, by 1513-1515 he has invented his own compasses of proportion as is confirmed by two notes on CA 157vb (425v)[190] and CA385ra (1064r).[191] In a third note on CA248ra (672r, c. 1513) he refers specifically to "a compass of proportionality" showing it both in profile and face on, noting that its central axis is moveable and that "this works in irrational proportionality."[192] By about 1515, on CA83va (225v) Leonardo notes that "With this [proposition] of the Elements one can give any proportion of a circle, rational as well as irrational."[193]
Here the reference to Elements is once again to his magnum opus, which began as Elements of machines. As Leonardo's work on geometrical transformation progresses he refers to individual books and sections by a variety of names. On CA128ra (353r, c. 1508), for instance, he refers to a "Book of equations"[194] (in the sense of equivalent shapes). On a number of occasions he refers to treatises "On transmutation" (i.e. transformation)[195] and "On the geometrical game."[196] A note on CA45va (124v, 1515-1516) records the beginning of this latter project: "Having finished giving various means of squaring the circle, i.e. giving quadrates of equal size to those of the circle, and having given rules to proceed to infinity, at present I am beginning the book On the Geometrical Game and I shall once again give the means of infinite progression."[197] Later, on CA167r (455r, c. 1517-1518), he refers to a "Treatise on continuous quantity."[198] As early as 1508-1510, however, he refers to a work on "Curvilinear geometrical elements."[199] By 1513 he is referring to specific propositions in a work entitled Elements: a "first proposition[200]," a "fifth proposition[201]," the "43rd proposition of the first book[202]," the "last proposition of the second book."[203] All this points unequivocally to a much more systematic approach than has thus far been suspected. And this is confirmed by a passage on CA170ra (463v, c. 1516):
Many of these curvilinear circles of mine can be squared in themselves with the transmutation of their proper parts within their whole and there are many which cannot be squared with their own parts, but with parts taken from other surfaces produce quadrates equal to themselves. And with this I am composing my last work of 113 books in which 33 different ways are given of making rectilinear quadrates equal to circles, i.e. equal in quantity.[204]
An extraordinary picture thus emerges. Leonardo, who is frequently pictured as a chaotic amateur or even dismissed as a craftsman working in an intellectual vacuum, was engaged in a project the scope, coherence and system of which had never before been seen. The regularity of machines convinced him that there were a limited number of principles which could be identified. He found 21. Reuleaux, more than three and a half centuries later, was able to find one more.[205] While Leonardo was searching for these principles he became convinced that there were four basic powers underlying these: weight, motion, force and percussion. At first he limited his study mainly to static conditions, focussing on weight, using instruments to create model situations by means of which to test claims made within the abaco tradition. This led to his studies in Forster II.
Meanwhile, as his study of anatomy progressed, he developed a method of presentation based on Ptolemy's Geography. Just as Ptolemy started with the world followed by the provinces, so too did Leonardo begin with the whole human body followed by its parts.[206] Wishing to account for the principles of human movement, Leonardo focussed attention on two other powers: motion and force. By 1503, he was writing his treatise "On local motion, force and weight"[207] and this evolved into his Elements of machines, which he planned to serve as an introduction to his anatomical studies.[208]
As the scope of his vision widened so too did his search for original sources. In the period 1505-1508 we find translations from Jordanus Nemorarius' Elementa, De ratione ponderis and Liber de ponderibus, on CA154ra-va (416rv).[209] The latter of these texts is also cited elsewhere as on CA124ra (342r, c. 1508).[210] In this period he also studied Archimedes[211], Theodosius[212], an unidentified Zenofonte[213], and continued, of course, with his studies of Euclid. By this time he became aware also that if instruments were fundamental in providing model cases for testing propositions concerning nature, instruments were equally crucial in actually representing and demonstrating geometrically the principles involved. So what had begun as his Elements of machines led to a new branch involving Elements of geometry which was quite distinct from Euclid. Where Euclid used theoretical propositions in which diagrams were of incidental significance, Leonardo emphasized practical propositions in which diagrams played a fundamental role, functioning as demonstrations and sometimes even replacing verbal claims. Hence, whereas Euclid focussed on idealized verbal propositions, Leonardo emphasized constructed visible demonstrations. Euclid's aim was to catalogue the rules of static geometrical shapes. Leonardo's goal was to discover the systematic laws of how geometrical shapes could be transformed. He was not just interested in finding some handy solution. He wanted to find all possible solutions and, as we have seen, found 33 alternatives.
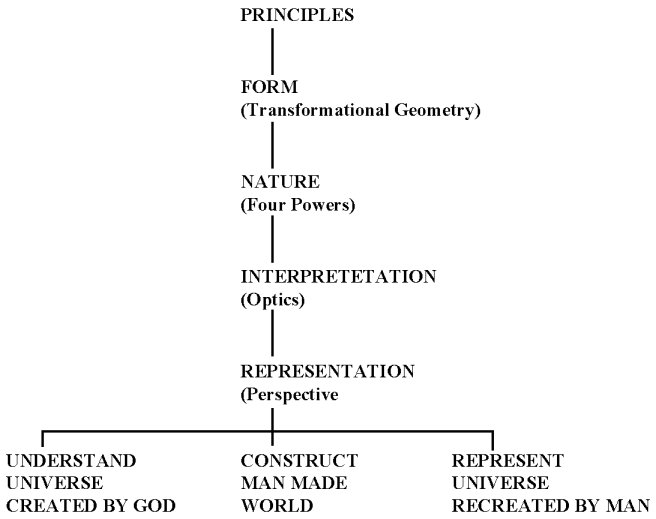
Leonardo's work on the Elements of machines and what might be termed his Elements of mechanical geometry thus became two parts of a single vision: to explain the created universe in terms of a constructed universe, that was simultaneously mechanical, geometrical, visible and therefore experimentally testable and capable of being both recorded and represented (fig. 7). That this second part of this project alone involved 133 books, in the sense of chapters, gives a sense of the enormity of this plan. The modern mind may see something manic in Leonardo's project and be tempted to dismiss it as over ambitious. To do so, however, would be to overlook the extraordinary optimism that made possible the Renaissance.